Importance Sampling in Off-Policy Reinforcement Learning Algorithms
Importance sampling is a technique often used in off-policy reinforcement learning algorithms. Off-policy algorithms are characterized by the use of two policies. One that is used to collect data through interaction with the environment, called the behavior policy. And another that is being learned, called the target policy. Since the policy used to generate learning data is different from that which is being learned, the data must be adjusted before they can be used to improve the target policy. This is where importance sampling comes into play.
The purpose of importance sampling is to estimate expected values under one distribution given samples from another. Before diving into the detail of applying importance sampling in off-policy algorithms, let us examine the technique with a simple example. Consider the following probability distributions, \(f(x)\) and \(g(x)\).
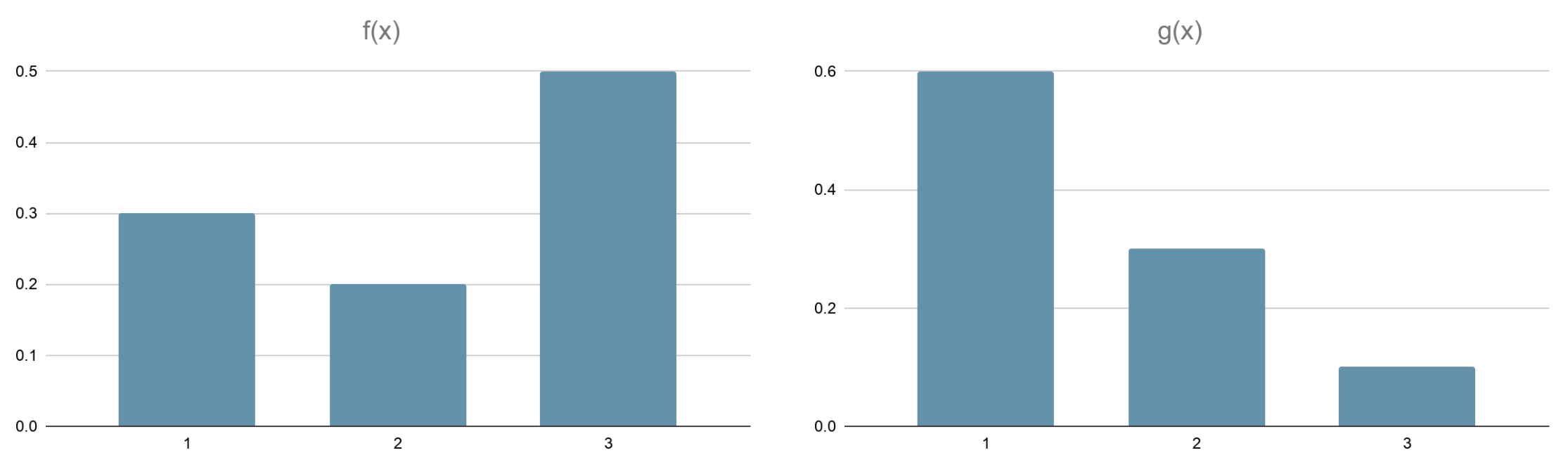
The expected value \(\textbf{E}_g[X]=\sum_x x g(x) = \sum_x x \frac{g(x)}{f(x)} f(x) = \textbf{E}_f[x\frac{g(x)}{f(x)}]\) can be approximated by \(\frac{1}{n}\sum_{i=1}^{n} x_i\frac{g(x_i)}{f(x_i)}\). The \(\frac{g(x_i)}{f(x_i)}\) part in the summation is called the importance-sampling ratio. As long as the importance-sampling ratios are known, we can estimate the value of \(\textbf{E}_g[X]\) with samples obtained from the other distribution, \(f(x)\). In this example, the sampling ratio corresponding to \(x_i=1\) is \(\frac{g(1)}{f(1)}=\frac{0.6}{0.3}=2\). Thus, if the samples generated under \(f(x)\) are \(2,3,3,1,3,3\), the estimate of \(\textbf{E}_g[X]\) would be \(\frac{1}{6}(1\cdot 2+2\cdot 1.5 + 3\cdot 0.2\cdot 4) = 1.233\).
Application of Importance Sampling in Off-policy Learning
Starting in state \(S_t\) and following the target policy \(\pi\), a subsequent state-action trajectory \(A_t, S_{t+1}, A_{t+1}, ..., S_T\) has probability
\[\begin{align*}&\textbf{P}_\pi[A_t, S_{t+1}, A_{t+1}, ..., S_T \mid S_t]\\ =&\pi(A_t\mid S_t)p(S_{t+1}\mid S_t, A_t)\pi(A_{t+1}\mid S_{t+1})...p(S_T \mid S_{T-1}, A_{T-1})\\ =&\prod_{k=t}^{T-1} {\pi(A_k\mid S_k)} {p(S_k+1\mid S_k, A_k)}\end{align*}\]Similarly, the probability of a state-action trajectory \(A_t, S_{t+1}, A_{t+1}, ..., S_T\) if we follow the behavior policy \(b\) is
\[\begin{align*}&\textbf{P}_b[A_t, S_{t+1}, A_{t+1}, ..., S_T \mid S_t]\\ =&\prod_{k=t}^{T-1} {b(A_k\mid S_k)} {p(S_k+1\mid S_k, A_k)}\end{align*}\]During off-policy learning, samples are generated by interacting with the environment according to the behavior policy \(b\). The sampled returns have the expectation \(\textbf{E}[G_t\mid S_t=s]=v_b(s) \neq v_\pi(s)\). To estimate the desired expected return \(v_\pi(s)\) under the target policy, we first calculate the importance-sampling ratio
\[\begin{align*} \rho_{t: T-1}= &\frac{\textbf{P}_\pi[A_t, S_{t+1}, A_{t+1}, ..., S_T \mid S_t]}{\textbf{P}_b[A_t, S_{t+1}, A_{t+1}, ..., S_T \mid S_t]}\\ = &\frac{\prod_{k=t}^{T-1} {\pi(A_k\mid S_k)} {p(S_k+1\mid S_k, A_k)}}{\prod_{k=t}^{T-1} {b(A_k\mid S_k)} {p(S_k+1\mid S_k, A_k)}}\\ = &\prod_{k=t}^{T-1}\frac{\pi(A_k\mid S_k)}{b(A_k\mid S_k)} \end{align*}\]We can now estimate a state value \(v_\pi(s)\) by averaging the returns with the importance-sampling ratio \(\rho_{t: T-1}\)
\[v_\pi(s)=\frac{\sum_{t: \mathbb{T}(s)}\rho_{t:T(t)-1}G_t}{|\mathbb{T}(s)|}\]where \(\mathbb{T}(s) = \{t \mid S_t = s\}\).
References
-
Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2017.
-
An introduction to importance sampling by Ben Lambert (YouTube video)