Introduction

Like Monte Carlo methods, TD methods can learn directly from raw experience without a model (model-free) of the environment’s dynamics. Like DP, TD methods update estimates based in part on other learned estimates, without waiting for a final outcome (they bootstrap).

6.1 TD Prediction

  • Every-visit Monte Carlo update for nonstationary environments
\[\newcommand{\S}{\mathcal{S}} \newcommand{\A}{\mathcal{A}} \newcommand{\R}{\mathcal{R}} \newcommand{\E}{\mathrm{E}} \newcommand{\deq}{\dot{=}} \newcommand{\argmax}[1]{\text{argmax}_{#1} \text{ }} \newcommand{\eps}{\varepsilon} \newcommand{\N}{\text{Normal}} \newcommand{\p}{\rho} \newcommand{\T}{\mathbb{T}} V(S_t)\leftarrow V(S_t)+\alpha[G_t-V(S_t)]\]
  • Simple TD update
\[V(S_t)\leftarrow V(S_t) +\alpha[R_{t+1}+\gamma V(S_{t+1})-V(S_t)]\]

  • TD(0)

  • TD error

\[\delta_t = R_{t+1+\gamma V(S_{t+1}-V(S_t))}\]
  • TD methods have an advantage over DP methods in that they do no require a model of the environment.
  • With Monte Carlo methods one must wait until the end of an episode, because only then is the return known, whereas with TD methods one need wait only one time step.

6.4 Sarsa: On-policy TD Control

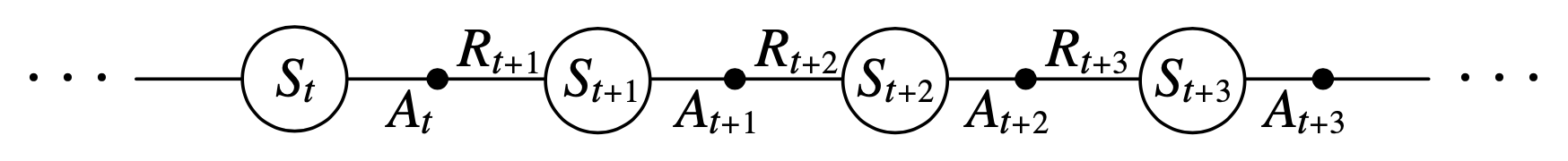
  • Consider transitions from state–action pair to state–action pair, and learn the values of state–action pairs.
\[Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha[R_{t+1}+\gamma Q(S_{t+1}, A_{t+1})-Q(S_t,A_t)]\]

  • The rule uses every element of the quintuple of events, $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$, that make up a transition from one state-action pair to the next.

  • Guaranteed to converge to an optimal policy and action-value function as long as all state-action pairs are visited an infinite number of times and the policy converges in the limit to the greedy policy.

6.5 Q-learning: Off-policy TD Control

\[Q(S_t,A_t) \leftarrow Q(S_t,A_t)+\alpha[R_{t+1}+\gamma \max_a Q(S_{t+1},a)-Q(S_t, A_t)]\]
  • In this case, the learned action-value function, $Q$, directly approximates $q_*$
  • Guaranteed to converge to $q_*$ if every state-action is visited an infinite number of times

6.6 Expected SARSA

  • Consider the learning algorithm that is just like Q-learning except that instead of the maximum over next state–action pairs it uses the expected value, taking into account how likely each action is under the current policy.
\[\begin{align*} Q(S_t, A_t) &\leftarrow Q(S_t, A_t)+\alpha[R_{t+1}+\gamma \E_\pi[Q(S_{t+1},A_{t+1})\mid S_{t+1}]-Q(S_t, A_t)]\\ &\leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma \sum_a \pi(a\mid S_{t+1})Q(S_{t+1}, a)-Q(S_t, A_t)] \end{align*}\]

6.7 Maximization Bias and Double Learning

  • In Q-learning and Sarsa, a maximum over estimated values is used implicitly as an estimate of the maximum value, which can lead to a significant positive bias.
  • Consider a single state $s$ where there are many actions $a$ whose true values, $q(s,a)$, are all zero but whose estimated values, $Q(s,a)$, are uncertain and thus distributed some above and some below zero. The maximum of the true values is zero, but the maximum of the estimates is positive, a positive bias.
  • There will be a positive maximization bias if we use the maximum of the estimates as an estimate of the maximum of the true values.
  • Suppose we divided the plays in two sets and used them to learn two independent estimates, $Q_1(a)$ and $Q_2(a)$, each an estimate of the true value $q(a)$, for all $a\in \A$. We could then use $Q_1$ to determine the maximizing action $ A^* = \argmax{a} Q_1(a)$, and $Q_2$ to provide the estimate of its value, $Q_2(A^* )$. This estimate will be unbiased in the sense that $\E[Q_2(A^* )]=q(A^* )$.
  • Double Q-learning update
\[Q_1(S_t,A_t)\leftarrow Q_1(S_t,A_t) + \alpha[R_{t+1} +\gamma Q_2(S_{t+1}, \argmax{a} Q_1(S_{t+1},a)) -Q_1(S_t,A_t)]\]
  • Double Q-learning algorithm

Games, Afterstates, and Other Special Cases

  • Afterstate value function: State-value function that evaluates state after the agent has made its move.
  • GPI still applies to afterstate methods.


References

  1. Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2017.